Double Counting과 Harmonic Lemma

※ 이 글을 읽기 전에, 제가 2년도 더 전에 타 블로그에서 썼던 글을 먼저 읽고 오시면 더 좋습니다.

 

▣ 정수론 시리즈 ─ 순서대로 읽으시는 걸 추천합니다.

1. 뫼비우스 함수와 디리클레 합성곱

2. Double Counting과 Harmonic Lemma (현재 글)

3. 곱셈적 함수 테이블 만들기

4. Mertens Trick (xudyh's sieve)

 

Intro

  이번 글은 문제 하나를 소개하며 시작하고자 한다.

 

  2019년도 NYPC에서 다음과 같은 문제가 출제된 적이 있었다.

NYPC 2019 Day 2 - 9번. 약수 문제
두 자연수 $a$, $b$가 주어질 때, $a$ 이상 $b$ 이하의 모든 양의 정수의 약수의 개수의 합을 구하시오.
다시 말해, $\sum\limits _{n=a}^{b} \tau(n)$의 값을 구하시오.

 

  문제는 지극히 간단하다. 제한 시간 1초에, $a$와 $b$의 범위가 $1$ 이상 $10^{12}$(1조) 이하라는 점만 뺀다면 말이다! 이 무시무시하게 큰 입력 범위 때문에 문제의 난이도가 치솟았고, NYPC에 지원한 많은 코딩 꿈나무들이 좌절을 겪게 되었다……는 농담이고, 실은 이 문제가 서브태스크 문제였던 데다가, 저 입력 범위를 가진 TC에 배정된 점수가 엄청 작아서 못 풀었어도 별 영향은 없었을 것이다. (^^)

 

  그런데…….

 

그래서 어떻게 해결할 것인가?

  그래서 저 무지막지한 범위의 구간이 입력되었을 때 문제를 해결하려면 어떻게 해야 하는가? 우선, 편의를 위해 문제를 구간이 $1$ 이상 $N$ 이하의 형태로만 주어지는 것으로 살짝 고쳐 보자. 그러면 $a$ 이상 $b$ 이하라는 구간은 $1$ 이상 $b$ 이하 구간에서 $1$ 이상 $a-1$ 이하 구간을 제외한 것으로 생각할 수 있다. (참고로 이렇게 구간의 한쪽 끝을 고정시키는 건 상당히 자주 쓰이는 아이디어이기 때문에 알아 두면 좋다.) 이때

 

$S(N):= \sum\limits _{n=1}^N \tau(n)=$ $1$ 이상 $N$ 이하의 양의 정수의 약수 개수의 합

 

이라 하면, 문제에서 구하는 값은 $S(b) - S(a-1)$이 된다. 만약 $N$의 크기를 신경쓰지 않는다면, naive하게 주어진 구간 내에 있는 모든 정수들의 약수의 개수를 일일이 구하는 풀이가 가장 먼저 떠오를 것이다. 그러나 정수 $n$의 약수의 개수를 구하는 데에 $\mathcal O(\sqrt n)$번의 연산이 필요하므로 총 시간복잡도는 $\color{plum}{\mathcal O(N^{\frac{3}{2}})}$가 되어, $1$과 $10^{12}$가 입력으로 주어진다면 70년 정도 지나서야 답이 나올 것이다.(...) 사실 아무 것도 안 하고 구간 내의 모든 수를 보기만 해도 $\mathcal O(N)$의 시간복잡도를 가지기 때문에, 수 하나하나마다 일일이 무언가를 하려는 순간부터 문제를 풀 수 없다. 정직하게 약수를 구해서는 문제를 풀 수 없다면, 문제를 전혀 다른 방법으로 접근해야 하는 것일까?

 

$\mathcal O(N)$ Solution: Double Counting

  더블 카운팅(Double Counting)이라는 개념이 있다. 이름 그대로 어떠한 대상을 두 가지 이상의 방법으로 계산한다는 뜻이다. 정말 쉬운 예로 직사각형 형태로 배열되어 있는 물건의 개수를 가로 방향을 기준으로 세는 것과 세로 방향을 기준으로 세는 것이 있겠다. 물론 같은 대상을 계산하는 것이므로 결괏값은 계산하는 방법에 상관없이 항상 같아야 할 것이다. (그리고 조합론 쪽에서는 이를 증명에 이용하는 경우가 많다.) 그런데 어떤 대상을 계산하는 데 여러 방법이 존재하고, 우리는 그 대상을 어떻게든 계산해야 한다면 당연히 그중 제일 쉬운 방법으로 계산하는 것이 이득이지 않겠는가?

 

  문제로 돌아와서, 약수 문제를 다르게 보려면 배수 문제로 바꾸는 게 제일 합리적이다. 약수와 배수, 둘은 항상 붙어 다니는 개념들이니까. 게다가, 어떤 수의 약수를 구하는 것보다 배수를 구하는 게 훨씬 쉽다!

 

[그림 1] 약수와 배수를 이용한 더블 카운팅

  [그림 1]을 보자. $1$부터 시작한 양의 정수들의 약수들을 줄마다 나열해 놓았는데, 우리는 지금 가로 방향의 파란 묶음들에 속한 수들의 총 개수를 구하려 한다. 그런데 이 값은 세로 방향의 빨간 묶음들에 속한 수들의 총 개수로도 구할 수 있다는 게 보일 것이다. 그렇다면 각 빨간 묶음은 어떤 의미를 가지는가? 왼쪽에서 $k$번째 빨간 묶음에는 $k$만이 들어 있는데, [그림 1]이 약수를 나열한 것임을 상기하면 결국 $k$의 모든 배수들이 속해 있는 것과 동일하다! 즉 $k$번째 빨간 묶음에 속한 수의 개수는 '$1$부터 $N$까지의 수 중 $k$의 배수의 개수'와 같고, 이는 $\lfloor \frac{N}{k} \rfloor$로 나타낼 수 있다. 이때 빨간 묶음이 $1$이 속한 묶음부터 $N$이 속한 묶음까지 총 $N$개 있으므로

$$\therefore\, S(N) = \sum_{k=1}^N \left\lfloor \frac{N}{k} \right\rfloor \quad \cdots\ (\star)$$

 

  놀랍지 않은가? $\tau(n)$의 합이 이렇게 간단한 식으로 나오는 것이…! $(\star)$ 식은 $\color{magenta}{\mathcal O(N)}$의 시간복잡도를 가지므로, 컴퓨터를 1시간 남짓 돌린다면 답이 나올 것이다. 와우! 70년에서 많이도 줄였다. 하지만 제한 시간은 고작 1초다. 아니, 여기서 더 줄여야 한다고…?

$\mathcal O(\sqrt N)$ Solution: Harmonic Lemma

  이대로 있으면 죽도 밥도 안 된다. 영감을 얻기 위해, 위 식에서 시그마를 떼고 직접 계산해 보도록 하자. 적당히 $N = 10$으로 가정하고 계산해 보면 $$\begin{aligned}f(10) &= \left\lfloor \frac{10}{1} \right\rfloor + \left\lfloor \frac{10}{2} \right\rfloor + \cdots + \left\lfloor \frac{10}{10} \right\rfloor \\ &= 10 + 5 + 3 + 2 + 2 + 1 + 1 + 1 + 1 + 1 \\ &= 27\end{aligned}$$ 와 같이 될 것이다. 어라? 어째 뒤로 갈수록 똑같은 값을 가지는 항이 많이 보이는 듯하다. 그렇다면 같은 값을 가지는 항끼리 묶어서 계산하면 더 빨라지지 않을까? 여기서 중요해지는 것이 서로 다른 값의 개수와, 같은 값을 가지는 항들이 어떻게 분포할지다. 먼저 서로 다른 값의 개수에 대해서는, 고맙게도 Harmonic Lemma라는 보조정리가 답을 주고 있다.

Lemma. Harmonic Lemma
집합 $\left\{ \left\lfloor \dfrac{n}{k} \right\rfloor \biggr|\, 1 \le k \le n,\, k \in \mathbb{Z}^+ \right\}$의 원소의 개수는 $2\left\lfloor \sqrt n \right\rfloor$개 이하다.

 

Proof.  $1 \le k \le \left\lfloor \sqrt n \right\rfloor$일 경우, $k$가 $\left\lfloor \sqrt n \right\rfloor$개라서 그에 대응되는 $\left\lfloor \dfrac{n}{k} \right\rfloor$ 역시 $\left\lfloor \sqrt n \right\rfloor$개 이하다. $\left\lfloor \sqrt n \right\rfloor < k \le n$일 경우, $\left\lfloor \dfrac{n}{k} \right\rfloor \le \left\lfloor \dfrac{n}{\left\lfloor \sqrt n \right\rfloor} \right\rfloor = \left\lfloor \sqrt n \right\rfloor$이므로 서로 다른 값의 개수($=$ 원소의 개수)는 $\left\lfloor \sqrt n \right\rfloor$개 이하다. 따라서 모든 원소의 개수는 $2\left\lfloor \sqrt n \right\rfloor$개 이하가 된다. (나아가 위 집합은 $\left\{ \left\lfloor \frac{n}{i} \right\rfloor \, \bigl| \, 1 \le i \le \left\lfloor \sqrt n \right\rfloor \right\} \,\cup \, \{ i\,\, \bigl| \, 1 \le i \le \left\lfloor \sqrt n \right\rfloor \}$로 표현 가능하다는 사실도 도출할 수 있다.)     $\square$

 

  따라서 같은 값끼리 묶을 경우 최대 $2\left\lfloor \sqrt n \right\rfloor$번의 계산만 하면 된다는 걸 알 수 있다! 남은 건 같은 값을 가지는 항의 분포인데, 이는 간단한 식 전개로 유도할 수 있다. $\lfloor \frac{n}{k} \rfloor = x$인 $k$의 범위를 생각하면,

$$\left\lfloor \frac{n}{k} \right\rfloor = x ~~~ \Rightarrow ~~~ x \le \frac{n}{k} < x+1  ~~~ \Rightarrow ~~~ \frac{n}{x+1} < k \le \frac{n}{x}$$

$$\therefore\, \left\lfloor \frac{n}{x+1} \right\rfloor < k \le \left\lfloor \frac{n}{x} \right\rfloor\ (\because\, k \in \mathbb{Z}^+)$$

 

즉 같은 값을 가지는 항이 연속된 구간으로 나오며, 그 구간의 양 끝은 $\lfloor \frac{n}{x} \rfloor$ 꼴로 나온다!

 

  지금까지의 논의를 $(\star)$ 식에 대입해 보자. $\lfloor \frac{N}{k} \rfloor$의 서로 다른 값을 내림차순으로 $a_1(=N)$, $a_2$, $\cdots$, $a_t(=1)$라고 하고, $\lfloor \frac{N}{k} \rfloor = a_i$인 $k$가 $s_i$ 이상 $e_i$ 이하 구간이라고 하자. 그렇다면 $$a_i = \left\lfloor \frac{N}{s_i} \right\rfloor,\ t \le 2{\left\lfloor \sqrt N \right\rfloor},\ s_i = e_{i-1} + 1,\ e_i = \left\lfloor \frac{N}{a_i} \right\rfloor = \left\lfloor \frac{N}{\lfloor N/s_i \rfloor} \right\rfloor$$가 성립한다(편의상 $e_0 = 0$이라 하자). 그리고 $(\star)$ 식은 $(e_i - s_i + 1)$개의 $a_i = \lfloor \frac{N}{s_i} \rfloor$를 더해가는 식으로 구할 수 있으므로…

$$\therefore\, S(N) = \sum_{i=1}^t {\left\lfloor \dfrac{N}{s_i} \right\rfloor} (e_i - s_i + 1)$$

 

  감격스럽게도, 우리는 방금 또 한 번의 위대한 진보를 이루어 냈다. 위 식의 시간복잡도는 $t \le 2\lfloor \sqrt N \rfloor$에 의해 $\color{red}{\mathcal O(\sqrt N)}$이 되고, 이는 $10^{12}$라는 흉악한(?) 입력이 들어와도 1초 내에 구할 수 있는 복잡도이다(넉넉잡아 10ms 이내로 답이 나올 것이다). 즉, 우리는 본 문제를 해결하였다! (짝짝짝…)

 

  위 내용을 바탕으로 작성한 최종 코드는 다음과 같다. (코드에서 i가 $s_i$, j가 $e_i$ 역할을 한다.)

#include <stdio.h>
#define lint long long

lint f(lint n) {
	lint i, j, ret = 0;
	for (i = 1; i <= n; i = j+1) {
		j = n / (n / i);
		ret += n / i * (j - i + 1);
	}
	return ret;
}

int main()
{
	lint a, b;
	scanf("%lld%lld", &a, &b);
	printf("%lld", f(b) - f(a-1));
	return 0;
}

 

Generalization

  그런데 고작 저 한 문제 풀려고 이 고생을 했다고 생각하면 아깝지 않은가? 위의 아이디어를 일반화해서 더 쓸모 있게 만들어 보자. 정수론에는 $\tau(n)$ 말고도 약수와 관련된 함수가 꽤나 있으며, 그런 함수들은 어떤 수론적 함수 $f$가 있어서 $\sum\limits _{d|n} f(d)$로 나타낼 수 있다. ($\tau(n)$의 경우, $f(d)=1$인 셈이다.) 그렇다면 $$\sum _{n=1}^N \sum _{d|n} f(d)$$의 값도 빠르게 구할 수 있을까?

 

  지금까지의 과정에서 중요하게 작용했던 아이디어를 생각해 보면, 1) 연속된 구간에서 약수를 가지고 노는 것은, 모든 수의 배수들을 가지고 노는 것으로 변환시킬 수 있다. 라는 것과 2) Harmonic Lemma를 통해 $\lfloor \frac{n}{k} \rfloor$ 꼴의 항들을 계산하는 시간복잡도를 줄였다. 는 것이다. 이를 한 번 더 그대로 적용하자.

 

[그림 2] 약수-배수 더블 카운팅의 일반화

  위 [그림 2]에서 보듯이, 우리는 파란 묶음에서 $f(d)$를 계산하여 합하는 게 목적인데 이는 빨간 묶음에서 $f(d)$를 계산하여 합하는 것과 같다. 그리고 위에서 말했던 대로, 왼쪽에서 $k$번째 빨간 묶음에 속한 각각의 $n$들은 모든 $k$의 배수들과 대응된다. 이때 $n=de$라고 하면 $1 \le n \le N$에서 $1 \le e \le \lfloor \frac{N}{d} \rfloor$가 되므로

$$\therefore\, \sum_{n=1}^N \sum_{d|n} f(d) = \sum_{d=1}^N \sum_{e=1}^{\left\lfloor \frac{N}{d} \right\rfloor} f(d) = \sum_{d=1}^N f(d) \sum_{e=1}^{\left\lfloor \frac{N}{d} \right\rfloor}1 = \sum_{d=1}^N f(d) \left\lfloor \frac{N}{d} \right\rfloor$$

 

  결국 더블 카운팅은 시그마의 순서를 바꾸는 효과를 낸다는 것을 알 수 있다. 아까와 마찬가지로 $\lfloor \frac{N}{d} \rfloor$의 서로 다른 값을 내림차순으로 $a_1$, $a_2$, $\cdots$, $a_t$라 하고, $\lfloor \frac{N}{d} \rfloor = a_i$인 $d$가 $s_i$ 이상 $e_i$ 이하 구간이라고 하면(여기서 $S_f (n) := \sum\limits _{k=1}^n f(k)$로 정의한다)

$$\begin{aligned} \therefore\, \sum_{n=1}^N \sum_{d|n} f(d) &= \sum_{d=1}^N f(d) \left\lfloor \frac{N}{d} \right\rfloor = \sum_{i=1}^t a_i \sum_{j=s_i}^{e_i} f(j) \\ &= \sum_{i=1}^t a_i (S_f(e_i) - S_f(s_i - 1)) \end{aligned}​$$

  이때 $S_f(n)$을 미리 전처리하거나 $\mathcal O(1)$에 구할 수 있다면, 위 식은 Harmonic Lemma에 의해 $\mathcal O(\sqrt N)$에 계산할 수 있다. 허나 아직 좋아하기는 이르다. 이전 글에서 소개한 디리클레 합성곱에 따르면 $\sum\limits _{d|n} f(d) = f \ast 1$ 아니던가? 그렇다면 또 일반화해서 $$S_{f \ast g}(N) = \sum _{n=1}^N \,(f \ast g)(n)$$ 도 빠르게 계산할 수 있을까? 물론 그 답은 Yes다! 한 번만 더 위 과정을 그대로 적용하면

$$\begin{aligned} S_{f \ast g}(N) &= \sum_{n=1}^N \sum_{d|n} f(d)g{\left( \frac{n}{d} \right)} = \sum_{d=1}^N \sum_{e=1}^{\left\lfloor \frac{N}{d} \right\rfloor} f(d)g(e)\\ &= \sum_{d=1}^N f(d) \sum_{e=1}^{\left\lfloor \frac{N}{d} \right\rfloor}g(e) = \sum_{d=1}^N f(d) S_g {\left( \left\lfloor \frac{N}{d} \right\rfloor \right)} \\ &= \sum_{i=1}^t S_g(a_i) (S_f(e_i) - S_f(s_i - 1)) \end{aligned}​$$

가 되고, 역시 $S_f$와 $S_g$를 $\mathcal O(1)$에 구할 수 있다면(혹은 전처리한다면) 마지막 식은 $\mathcal O(\sqrt N)$에 계산이 가능하다!

 

  다시 말해 디리클레 합성곱은 합성하는 두 함수의 부분합을 빠르게 구할 수 있다면 합성곱의 부분합 역시 naive한 방법보다 훨씬 빠르게 구할 수 있다는 장점이 있고, 많은 곱셈적 함수들이 디리클레 합성곱으로 표현되므로 여러 곱셈적 함수들의 부분합을 좀 더 효율적으로 구할 수 있게 된다. 한 예시로, $n$의 양의 약수의 합 $\sigma(n)$에 대해 $\sigma = {\rm Id} \ast 1$이므로 $\sigma(n)$의 부분합을 구하려면 위 식에 $f = {\rm Id}$, $g = 1$을 대입하면 그만이다. 이때 $S_f (n) = \frac{n(n+1)}{2}$, $S_g (n) = n$으로 $\mathcal O(1)$에 구할 수 있으므로 $\sigma(n)$의 부분합은 $\mathcal O(\sqrt N)$에 구할 수 있다. (코드를 스스로 작성해 보는 걸 추천한다.)

 

  그렇다면 반대로, 합성하는 두 함수 중 한 함수의 부분합과 합성곱의 부분합을 빠르게 구할 수 있을 때, 나머지 하나의 함수의 부분합도 좀 더 효율적으로 구할 수 있는가? 이에 대해서는 다음다음 글에서 알아보도록 하겠다….

 

  한편, Harmonic Lemma만으로도 일반화해 볼 부분이 있다. 우리는 $\lfloor \frac{n}{k} \rfloor$ 꼴의 합을 구하였는데, 그렇다면 어떤 두 양의 정수 $m$, $n$에 대해 $$\sum_{k=1}^{\min(m,\, n)} {\left\lfloor \frac{m}{k} \right\rfloor} {\left\lfloor \frac{n}{k} \right\rfloor}$$의 값도 $\mathcal O(\min(m,\, n))$보다 빠르게 계산 가능할까? 수직선에 $\lfloor \frac{m}{k} \rfloor$의 값이 같은 구간과 $\lfloor \frac{n}{k} \rfloor$의 값이 같은 구간을 "칼로 자른다"고 생각해 보면, Harmonic Lemma에 의해 최대 $2\left(\left\lfloor \sqrt m \right\rfloor + \left\lfloor \sqrt n \right\rfloor\right)$개의 '조각'이 나올 것이다. 그리고 조각 내의 $k$에 대해서는 ${\lfloor \frac{m}{k} \rfloor} {\lfloor \frac{n}{k} \rfloor}$의 값이 같으므로, 결국 위 식을 $\mathcal O(\sqrt m + \sqrt n)$에 계산할 수 있게 된다. 이때 각 구간의 시작값을 $i$라고 하면(초기에 $i=1$일 것이다) 끝값은 $\min \!\left({\left\lfloor \frac{m}{\lfloor m/i \rfloor} \right\rfloor},\, {\left\lfloor \frac{n}{\lfloor n/i \rfloor} \right\rfloor} \right)$가 될 것이다. 곱해진 항이 세 개 이상일 경우에도 마찬가지의 논리를 적용할 수 있으며, 이로써 우리는 일반화를 성공적으로 마쳤다!

 

  이렇게 문제 하나를 해결하는 과정을 통해 더블 카운팅과 Harmonic Lemma의 개념 및 그 응용과 일반화에 대해 속속들이 알아보았다. 다음 글에서는, 잠시 쉬어가는 느낌(?)으로 여러 곱셈적 함수들의 테이블(함숫값 리스트)을 만드는 방법에 대해서 알아볼 것이다.

 

 

─ To Be Continued…

 

 

---

더 나아가기

  위에서 $$S_{f \ast g}(N) = \sum_{d=1}^N f(d) \sum_{e=1}^{\left\lfloor \frac{N}{d} \right\rfloor} g(e)$$로 나타낼 수 있다고 했었다. 그런데 $f \ast g = g \ast f$라는 걸 생각해보면, 다음의 식이 성립한다는 걸 알 수 있다!

 

$$\sum_{d=1}^N f(d) \sum_{e=1}^{\left\lfloor \frac{N}{d} \right\rfloor} g(e) = \sum_{d=1}^N g(d) \sum_{e=1}^{\left\lfloor \frac{N}{d} \right\rfloor} f(e)$$

 

  위 식이 직관적으로 와닿지 않는다면, 다음 그림에서 빨간 묶음과 초록색 묶음을 잘 살펴 보고 스스로 깨달아 보자. (참고로 $d$와 $e$는 시그마에서의 변수일 뿐이기 때문에 서로 위치를 바꾸어도 상관없다는 점에 유의하라.)

 

[그림 3] 또 다른 더블 카운팅 방법

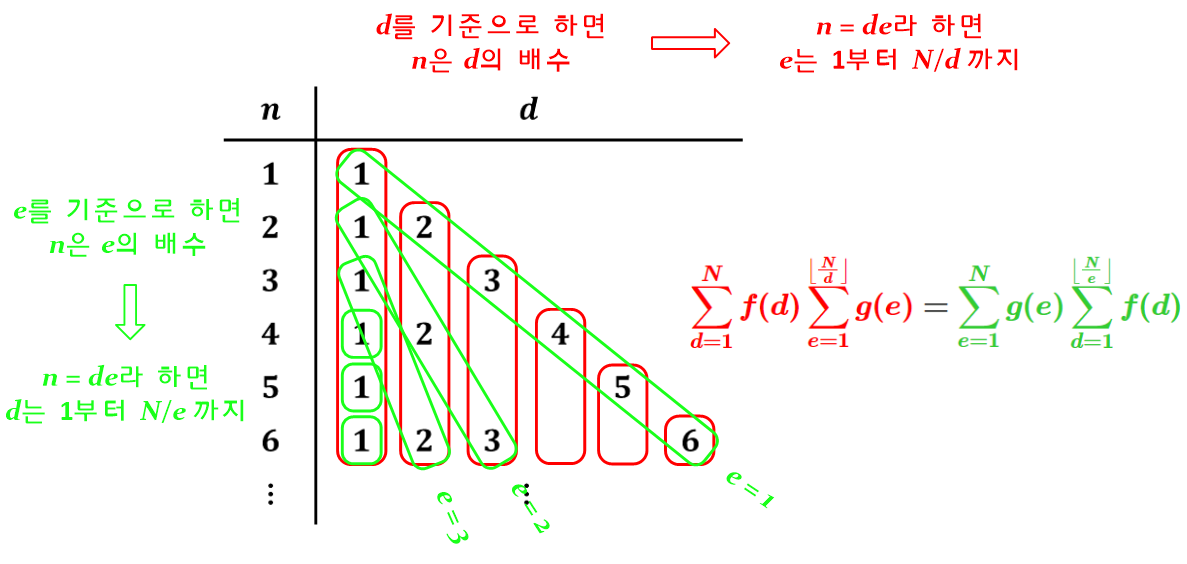
어떤가? 더블 카운팅이라는 개념과 좀 친근해진 듯한 느낌이 드는가? (^^)